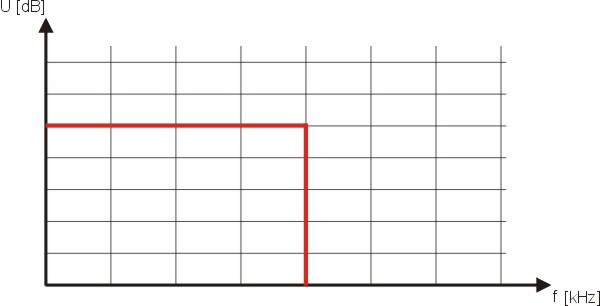
Abb. 1: Ideeller Kurvenverlauf beim Tiefpassfilter

Diesen Filter gibt es leider nicht. Aber man kann einen recht großen Aufwand betreiben, dass die Filtercharacteristik der idealen Kurve am nähesten kommt. Die Tief- oder Hochpassfilter werden nach Ordnungen und Art unterschieden. Eine RC-Kombinaton stellt einen Filter 1. Ordnung dar. Bei diesem ganz einfachen Filter beträgt der Abfall 20dB pro Dekade. Die Arten sind u.a.:

•  Filter mit kritischer Dämpfung
•  Butterworth Tiefpass
•  Bessel-Tiefpass
•  Tschebyscheff-Tiefpass, die sich in der Welligkeit unterscheiden
•  Tiefpass mit 0,5dB Welligkeit
•  Tiefpass mit 1dB Welligkeit
•  Tiefpass mit 2dB Welligkeit
•  Tiefpass mit 3dB Welligkeit

Diese Filter unterscheiden sich in ihrer Filtercharakteristik, also in ihrem Verhalten. Am Besten erkennt man dieses in der nächsten Abbildung. Dort sind alle Filter mit ihren Kurven zu sehen.

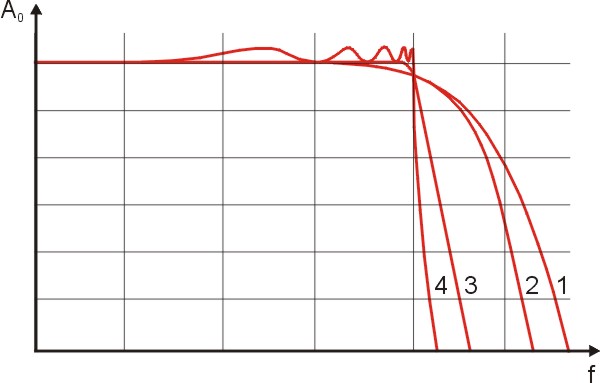
Abb. 2: Tiefpassfilter und ihre Kurven

Zu den Kurven:

Kurve Filtertyp 1  Tiefpass mit kritischer Dämpfung 2  Bessel-Tiefpass 3  Butterworth-Tiefpass 4  Tschebyscheff-Tiefpass (3dB Welligkeit)

Tab. 1: Koeffizienten für den Tiefpassfilter

Hier kann man erkennen, dass der Filter mit kritischer Dämpfung und der Bessel-Filter bis zur Grenzfrequenz, schön linear verlaufen, danach aber etwas flacher abfallen als die anderen beiden Filter. Der Butterworth-Filter geht auch noch sehr linear bis zur Grenzfrequenz heran, fällt aber nicht steil genug ab. Da ist der Tschebyscheff-Filter eben besser. Diesen steilen Abfall der Kurve, erkauft man sich hier mit einer gewissen Welligkeit, vor der Grenzfrequenz. Bei dem Stereocoder ist diese Welligkeit nicht ganz so wichtig. Wichtiger ist der steile Abfall der Kurve.

Auf der vorherigen erkennt man, dass der Tschebyscheff-Filter den steilsten Abfall der Kurve hat. Daher wird für den Stereocoder der Tschebyscheff-Filter ausgewählt. Jetzt bleibt noch zu klären, welche Welligkeit man nimmt. Mit zunehmender Welligkeit, wird auch der Abfall der Kurver, steiler. Es hat sich herausgestellt, dass eine 3dB Welligkeit (steilster Abfall) gar nicht ausreicht! Selbst bei diesem steilen Abfall der Kurve, würden noch zu viele Anteile bei 19kHz durchkommen. Welche Möglichkeiten gibt es noch?

• Grenzfrequenz von 15kHz auf 12kHz legen
Das ist eine schlechte Lösung. Die Höhen würden bedämpft werden. Das wird sich im Radio sehr schlecht anhören. Es fehlen dadurch die Höhen.
• Einen Tiefpass höhre Ordnung wählen
Das macht zwar mehr Arbeit, aber das kommt der idealen Übertragungskurve am Nächsten.

Durch Berechnungen hat sich herausgestellt, dass ein Tschebyscheff-Filter 10. Ordnung mit einer Welligkeit von 0,5dB, ausreicht.

Schaltet man 5 Filter 2. Ordnung hintereinander, so ergibt das ein Filter 10. Ordnung. Wichtig dabei ist, dass die Filter untereinander, entkoppelt werden. Das kann mit einem Impedanzwandler geschehen.

HINWEIS

Der Impedanzwandler wird der einfachheit halber so gezeichnet wie er in der Abb. 3 zu sehen ist. Real wird er aufgebaut wie in in diesem Popup-Fenster dargestellt wird. Dieser Impedanzwandler dreht das Ausgangssignal um 180°. Es kann alternativ auch der nichtinvertierende Impedanzwandler (Elektrometerverstärker) eingesetzt werden. Welcher nun hier eingesetzt ist egal, da die Phasenlage des NF-Signal keine Rolle spielt. Wichtig ist, dass beide Kanäle die gleiche Phasenlage besitzen.

Anforderung an die Schaltung

• Die Grenzfrequenz muss bei 15kHz liegen
• Die Verstärkung soll 1 sein
• Filterart: Tschebyscheff 10. Ordnung mit 0,5dB Welligkeit

Jetzt kommen wir zur Berechnung der Schaltung. Es wird der Filter 2. Ordnung berechnet. Den Filter 10. Ordnung bekommt man, indem 5 Filter der 2. Ordnung hintereinander geschaltet werden. Zwischen den Filtern wird ein Impedanzwandler geschaltet. Bei der Wahl der Koeffizienten muss bedacht werden, dass ein Filter 10. Ordnung berechnet wird. Dazu kommen wir gleich noch.

Tiefpassfilter zweiter Ordnung mit Mehrfachgegenkopplung

Hier das Schaltbild für ein Teilfilter, sowie des Impedanzwandlers:

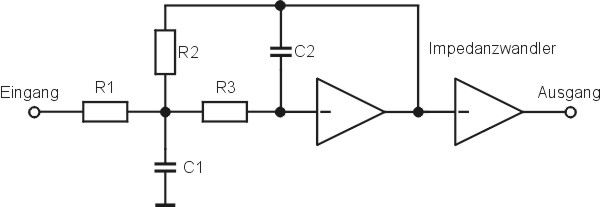
Abb. 3: Teilfilter mit nachgeschalteter Impedanzstufe

Das ist ein Tiefpass 2. Ordnung. Die Charakteristik des Filters, ob Bessel oder Tschebyscheff wird mit den Koeffizienten eingestellt. Zu diesen Werten kommen wir jetzt. Wir berechnen ein Filter der 10. Ordnung. Es wäre falsch, diese Koeffizienten für alle fünf Teilfilter zu nehmen! Daher müssen wir unsere Werte aus der nachfolgenden Tabelle entnehmen:

Kurzbezeichnung Wert a1 6,3648 b1 18,3695 a2 1,3582 b2 4,3453 a3 0,4822 b3 1,9440 a4 0,1994 b4 1,2520 a5 0,0563 b5 1,0263

Tab. 2: Koeffizienten für den Tiefpassfilter

Quelle: Tietze Schenk Halbleiter Schaltungstechnik

Kommen wir jetzt zur Berechnung der Schaltung:

Gefordert:

• Filterart = Tschebyscheff mit 0,5dB Welligkeit
• fg = 15kHz
• A0 = 1

Hier wird jetzt nur der erste Teilfilter berechnet. Wir haben in unserem Beispiel 5 Teilfilter. Es kommen für den ersten Teilfilter die Werte a1 und b1 in Frage. Diese werden aus der oberen Tabelle entnommen. Wenn der zweite Teilfilter berechnet wird, müssen die beiden Werte a2 und b2 herangezogen werden.
Noch eine Anmerkung zur Theorie und Praxis: In unserem Beispiel wird für den Kondensator C1 = 42nF berechent. Diesen Wert gibt es in der Praxis nicht. Wie man es in jeder Schule gelernt hat, wird daher der nächste in Frage kommende Wert gewählt. Das wäre in unserem Beispiel der Wert von 47nF. Und hier entsteht ein Problem: Der rechnerischen Werte stimmen nicht mit den tatsächlichen Werten überein. Das bedeutet: Der Filter wird nicht seine Grenzfrequenz bei exakt 15kHz haben. Dazu kommen noch Bauteiltoleranzen. Noch problematischer ist unsere Schaltung. Dadurch, dass die Werte nicht exakt stimmen, kann es sein, dass die Schaltung nicht richtig funktioniert. Es können Überschwinger auftreten o.ä. Faktoren. Bei einem Filter der 2. oder 4. Ordnung wäre das nicht so kritisch. Daher muss man hier etwas mehr Geduld aufbringen. Es kann sein, dass man hier verschieden Werte durchprobieren muss, um den Filter funktionsfähig zu machen. Dazu gehöhren auch ein gutes Layout, sowie gute, bzw. schnelle OAs. Ein einfacher 741 in der Standardausführung wird wahrscheinlich hier nicht ausreichen.
Leider muss ich dazu sagen, dass diese Schaltung nicht für Anfänger geeignet ist. Der Anfänger wird wahrscheinlich auch kein Oszilloskop besitzen, was hier jedoch Bedingung ist. Dazu kommt noch ein NF-Generator von ca. 20Hz bis ca. 25kHz. Dieses ist jedoch notwendig um die Filtercharacteristik zu überprüfen.
Jetzt zur Berechnung der Schaltung:

Die Formel für einen Tiefpass der 2. Ordnung lautet allgemein:

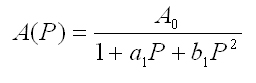
Abb. 4: Formel 1.1

In unsere Schaltung sind die Widerstände R1 bis R3, sowie die Kondensatoren C1 und C2. Diese finden sich in der Formel 1.2 wieder. Hier die genauere Darstellung:

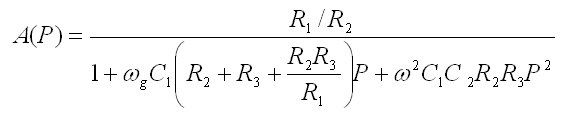
Abb. 5: Formel 1.2

Diese Formel wirkt recht kompliziert. Um es etwas einfacher zu gestalten werden die Widerstände R1, R2 und R3 zu einem gleichem Widerstand zusammengefasst. Weiterhin war gefordert, dass die Verstärkung 1 sein soll. Nach dieser Vereinfachung können wir die Formel von 1.2 jetzt so schreiben:

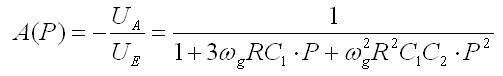
Abb. 6: Formel 1.3

Durch den Vergleich dieser Formel mit der Formel 1.1 ergeben sich die beiden Formeln 1.4 und 1.5.

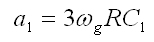
Abb. 7: Formel 1.4

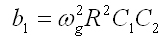
Abb. 8: Formel 1.5

Jetzt haben wir zwei Bestimmungsgleichungen und drei unbekannte Werte. Wir können oder müssen einen Wert wählen. Es ist besser einen Kondensator zu wählen, da die unterschiede in der Normreihe E6 zu hoch sind. Daher wird C2 mit 10nF gewählt.
Jetzt wird der Widerstand R (da alle Widerstände gleich sind, ist es hier R1, R2 und R3) ausgerechnet.

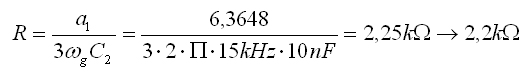
Abb. 9: Formel 1.6

Und hier wird der Kondensator C1 errechnet.

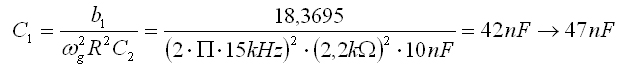
Abb. 10: Formel 1.7

Die Berechnung für den ersten Teilfilter ist hiermit fertig. Die anderen vier Filter werden nach dem gleichen Schema berechnet. Noch eine Anmerkung zum Schluss: Beim Aufbau der Schaltung sollte man eine Unterbrechungsmöglichkeit zwischen den Teilfiltern einbauen. So kann man hinter jedem Teilfilter mit einem Oszilloskop überprüfen, ob dieser Teilfilter korrekt arbeitet. Weiterhin kann man jede Filterstufe einzeln ansteuern. Das erleichtert die nachträgliche Fehlersuche.

HINWEIS

Jeder Teilfilter hat eine andere Grenzfrequenz! Wenn man jeden Frequenzgang eines Teilfilters multipliziert, dann kommt man auf die Grenzfrequenz von 15kHz. Bei der Überprüfung eines Teilfilters darf man sich daher nicht wundern, wenn die Grenzfrequenz nicht bei 15kHz liegt. Nur im Gesamten ist die Grenzfrequenz bei 15kHz.

Wer sich nicht zutraut den Filter 10. Ordnung nachzubauen oder auch die Messgeräte nicht besitzt, kann einen Filter mit Mehrfachgegenkopplung der 2. Ordnung nachbauen. Das ist Nachbausicher und dürfte jedem gelingen. Die Koeffizienten sind in der unterstehenden Tabelle aufgeführt. Die Schaltung ist wie ein Teilfilter, jedoch kann die Impedanzstufe weggelassen werden.

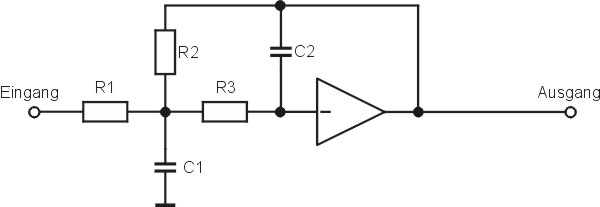
Abb. 11: Tiefpassfilter mit Mehrfachgegenkopplung 2. Ordnung

Und hier die beiden Koeffizienten:

Kurzbezeichnung Wert a1 1,3614 b1 1,3827

Tab. 3: Koeffizienten für den Tiefpassfilter

Quelle: Tietze Schenk Halbleiter Schaltungstechnik

Viel Spaß beim Nachbauen der Schaltung.